Guide: From NONMEM to Monolix
Welcome to Monolix! This guide is designed as a detailed reference for pharmacometricians transitioning from NONMEM. Instead of a linear walkthrough, this document is structured by topic, allowing you to look up a specific part of a NONMEM control stream (e.g., $OMEGA, $DES) and find its direct equivalent and implementation details in Monolix.
Our goal is to provide a comprehensive map from the NONMEM syntax you know to the integrated, graphical workflow of Monolix.
1. The Dataset ($INPUT)
The foundation of any model is the dataset. While NONMEM uses the $INPUT block with fixed column names, Monolix uses a flexible column tagging system. You can find detailed instructions on how to load a dataset in Monolix here.
Basic Column Mapping
When you load a dataset in Monolix, you assign a functional type to each column.
NONMEM Column | Monolix Column Type | Notes |
|---|---|---|
|
| Individual identifier. |
|
| Time of the record. |
|
| The dependent variable (e.g., concentration). |
|
| Dose amount. |
|
| Use for infusions. |
|
| Event identifier (e.g., 1 for dose, 0 for observation). |
|
| Marks records to ignore in the analysis. |
| Same names | Function identically for steady-state, inter-dose interval, and additional doses. |
Covariates |
| Tag as |
You can find more information about all the column types available in Monolix here.
The CMT Column
The CMT column in NONMEM is often used for multiple purposes. Monolix separates these functions for clarity:
To distinguish different observation types (e.g.,
CMT=2for PK,CMT=3for a PD biomarker): Tag theCMTcolumn as OBSERVATION ID.To direct doses to different compartments (e.g.,
CMT=1for IV,CMT=2for oral): Tag theCMTcolumn as ADMINISTRATION ID.If
CMTis used for both: You must split it into two separate columns in your dataset before loading it into Monolix—one for observation types and one for administration types.
BLQ Data
Handling data below the limit of quantification (BLQ) is vastly simplified.
In NONMEM: You must implement the M3/M4 method manually with complex
IF/THENlogic in the$ERRORblock to calculate the likelihood of an observation being censored.In Monolix: The process is entirely graphical:
Create a flag column in your dataset (e.g.,
BLQ) with1for censored observations and0for non-censored.In the rows where
BLQ=1, set theDVcolumn to the value of the limit of quantification (LOQ).In the Monolix Data tab, tag your
BLQcolumn as Censoring.
M3 vs. M4 Method: Monolix automatically selects the method. If you provide a
LIMITcolumn in your dataset where the value is0for censored data, the M4 method is used. Otherwise, the M3 method is used by default.
Filtering Data ($IGNORE)
To replicate NONMEM's $IGNORE statement, use the Filter feature in the Monolix Data tab. You can build complex rules to exclude individuals or specific records (e.g., DOSE == 0 to exclude a placebo arm).
Example:
NONMEM | Monolix |
|---|---|
CODE
|  |
Time-Varying Covariates (Regressors)
There is a critical difference in how time-varying covariates are handled between data points:
NONMEM: Uses "next value carried backward."
Monolix: Uses "last observation carried forward" by default. You can also select "linear interpolation" as an alternative method in the data formatting options. If the exact timing of a covariate's effect is critical, you may need to shift the values in your regressor column by one row in the dataset to achieve the same behavior as in NONMEM.
2. The Structural Model ($PK, $DES)
This is where you define your model's equations. In Monolix, this is done in the model file, written in the MLXTRAN language. How to choose a model file in Monolix is explained here.
Using the Library ($SUBROUTINES)
The easiest approach is to select a model from Monolix's extensive library. This is the equivalent of using an ADVAN routine and is the recommended starting point. The library contains validated models for PK, PD, TMDD, TTE, and more.
Example:
NONMEM | Monolix |
|---|---|
| Library model (V, Cl) |
Writing Custom Models Using ODEs
ODE Systems (from $DES)
You can often copy-paste your NONMEM ODEs into the EQUATION section of a model file with minor syntax changes.
NONMEM Syntax | Monolix (MLXTRAN) Syntax | Description |
|---|---|---|
|
| The derivative is defined using the |
|
| Variable names do not use parentheses for indexing. |
Initial condition in |
| Initial conditions are explicitly defined using the |
|
| The standard |
|
| Standard mathematical functions are written in lowercase. |
CODE
|
CODE
| Syntax differences for IF/ELSE statements:
|
ODE Solver Settings
To control the ODE solver (equivalent to $ADVAN... TOL=...), you can add keywords to the EQUATION section of your model file:
Solver Type:
odeType = stiffforces the use of a stiff solver, equivalent to$ADVAN13. The default is a non-stiff solver.Solver Tolerance: You can adjust the relative and absolute tolerance:
odeRelTol = 1e-6(this is the default value)odeAbsTol = 1e-9(this is the default value)
Example:
NONMEM | Monolix |
|---|---|
|
|
Dosing and Model Inputs (depot() macro)
The depot() macro is a powerful tool that replaces much of the logic from $PK or $MODEL. It links doses from the dataset to your model variables. You can find all the options available when using the depot macro here.
; This single line handles an oral dose with a lag time,
; bioavailability and first order absorption
depot(target=Aa, Tlag=Tlag, p=F, ka=ka)This is far more explicit and readable than NONMEM's implicit compartment-based dosing.
Compartment Definitions
Parts of the NONMEM control stream that define compartments and look like this can be completely omitted from the Monolix structural model:
$MODEL
COMP = (DEPOT, DEFDOSE)
COMP = (TDA)Transit Compartments
This is a prime example of Monolix's simplification:
NONMEM | Monolix |
|---|---|
You must manually code the gamma function approximation, a complex and error-prone task. | Simply add two keywords to the
CODE
Monolix uses the same analytical solution automatically in the background. |
Model Outputs and Error Logic (from $ERROR)
The complex logic in a NONMEM $ERROR block is split into two clear parts in Monolix:
Defining Outputs: You declare your model outputs in the
OUTPUTsection of the MLXTRAN file:CODEOUTPUT: output = {Cc, E}Mapping Outputs: In the GUI, you graphically map each model output to its corresponding
OBSERVATION ID. This completely replaces the need forIF (CMT.EQ.2) THEN ...statements. Residuals (RES,WRES) are calculated automatically and do not need to be coded.
3. The Statistical Model: ($THETA, $OMEGA, $SIGMA, Covariates)
This is where the Monolix workflow differs most from NONMEM. All aspects of the statistical model are defined visually in the Statistical Model & Tasks tab.
Model Parameters ($THETA, $OMEGA, $SIGMA)
Fixed Effects ($THETA)
These are the population typical values (_pop) for each parameter in your model (e.g., V_pop, Cl_pop). They are defined in the input section of the structural model file.
Random Effects ($OMEGA)
To add inter-individual variability (an ETA), simply check the Random Effect box for a parameter. Select the parameter distribution from the dropdown menu (choose between lognormal, normal and logitnormal).
NONMEM | Monolix |
|---|---|
CODE
| 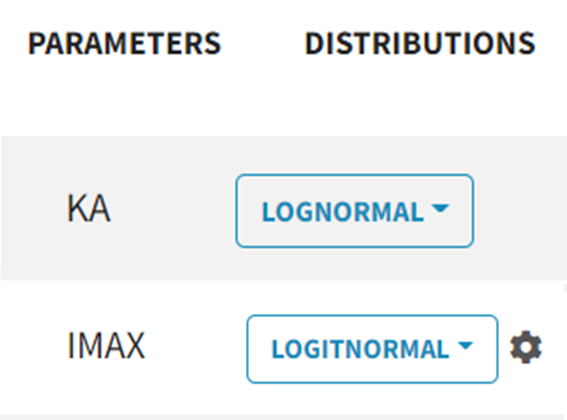 |
If the parameter distribution is not available (e.g., proportional or Box-Cox distribution), it has to be implemented by separating fixed and random effects:
NONMEM | Monolix |
|---|---|
CODE
|
CODE
|
Residual Error ($SIGMA)
The $ERROR block's error definition is replaced by a dropdown menu for each observation type, where you can select proportional, constant, combined1, combined2.
Examples:
NONMEM | Monolix |
|---|---|
CODE
| 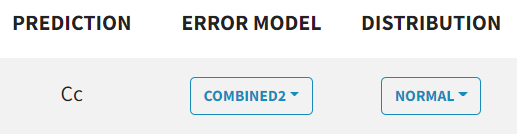 |
CODE
| 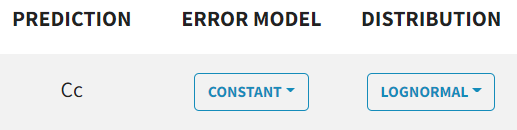 |
Covariate Models
How you translate a continuous covariate relationship depends on the mathematical form.
Categorical covariates
Monolix simplifies the implementation of categorical covariates by replacing NONMEM's manual IF/THEN logic with a graphical approach.
In NONMEM, you typically code the effect of a categorical covariate explicitly:
IF (SEX.EQ.0) THEN
TVCL = THETA(1)
ELSE
TVCL = THETA(2)
ENDIFOr, for a multiplicative effect on a log-normal parameter: TVCL = THETA(1) * THETA(2)**SEX.
The translation in Monolix involves two simple steps:
Tag the Covariate: In the Data tab, identify your categorical variable column (e.g.,
SEX) and tag it as a CATEGORICAL COVARIATE. Monolix will automatically detect the different categories (e.g., 0 and 1, or F and M).Add the Effect: In the Statistical Model tab, select the parameter you want the covariate to act on (e.g.,
Cl). Click to addSEXas a covariate.
Monolix automatically estimates a typical value (_pop parameter) for the reference category and a beta coefficient for the effect of each other category.
For example, the NONMEM code TVCL = THETA(1) * THETA(2)**SEX is equivalent to the Monolix formula:
|
|
Here, corresponds to
THETA(1) (the typical clearance for the reference category, SEX=0), and corresponds to
log(THETA(2)) (the log of the multiplicative factor for SEX=1). You don't need to write this equation; Monolix builds it for you.
Continuous Covariates - Exponential Relationship
This is the default for log-normally distributed parameters in Monolix and is the most common case.
Formula:
NONMEM Equivalent:
TVCL = THETA(1) * EXP(THETA(2)*WT)How to implement: Simply add the covariate to the parameter in the GUI by selecting the checkbox under
WTand next toClin the Statistical model & Tasks tab. Monolix defaults to this linear relationship on the log-transformed parameter.
Continuous Covariates - Power-Law Relationship
This is another common case.
Formula:
NONMEM Equivalent:
TVCL = THETA(1) * (WT/70)**THETA(2)How to implement:
Click on the name of the covariate
WTin the Statistical model & Tasks tab and then select “Add log-transformed”.Covariate
logtWTwill appear. Monolix will normalize the covariate when transforming using the weighted mean of the dataset values of that covariate. If you want to change the value by which the covariate is normalized, you can click on the name of the covariate and select “Edit”.You can add the covariate by clicking on the checkbox next to
Cland underlogtWT. Adding a log-transformed covariate is equivalent to using the power-law relationship for the covariate effect:
Other Relationships
For any relationship that cannot be built in the GUI (e.g., a sigmoid Emax model, a time-varying covariate effect), you must implement it directly in the structural model file.
Tag the covariate as a
REGRESSORin the Data tab. This makes its value available at each time point within the model.Implement the formula in the MLXTRAN code. List the regressor as an input and write the custom equation.
CODE[LONGITUDINAL] input = {Cl_pop, ..., mycov} mycov = {use=regressor} EQUATION: ; Custom relationship implemented directly tvCl = Cl_pop * (1 + (Emax * mycov) / (EC50 + mycov)) ...
More detailed information about custom covariate-parameter relationships: Complex covariate-parameter relationships.
Inter-Occasion Variability (IOV)
NONMEM | Monolix |
|---|---|
This requires a complex implementation with separate |
|
4. Initial Estimates and Estimation
Setting initial estimates requires careful attention to the differences in statistical definitions between the two platforms.
Fixed Effects ($THETA)
These are generally straightforward. Enter the THETA values as initial estimates for the _pop parameters. Be careful with transformations. For a NONMEM covariate model like TVCL = THETA(1) * THETA(2)**SEX, the corresponding Monolix parameter beta_Cl_SEX is actually log(THETA(2)). So if THETA(2)=1, beta_Cl_SEX=0.
Random Effects ($OMEGA and $SIGMA)
Variance vs. Standard Deviation: NONMEM's
$OMEGAand$SIGMAblocks define variances. Monolix works with standard deviations. To convert, use the formula:Covariance vs. Correlation: NONMEM's
$BLOCKstatement defines covariances. Monolix uses correlation coefficients (rho), a value between -1 and 1. To convert, use the formula:
Pro-Tip: For estimation, it is often sufficient to set the initial correlation value to 0 and let Monolix estimate it.
Fixed Parameters
In Monolix, parameters are fixed in the Initial estimates tab by clicking on the gear icon ![]() next to initial estimates and selecting “Fixed”.
next to initial estimates and selecting “Fixed”.
NONMEM | Monolix |
|---|---|
CODE
| 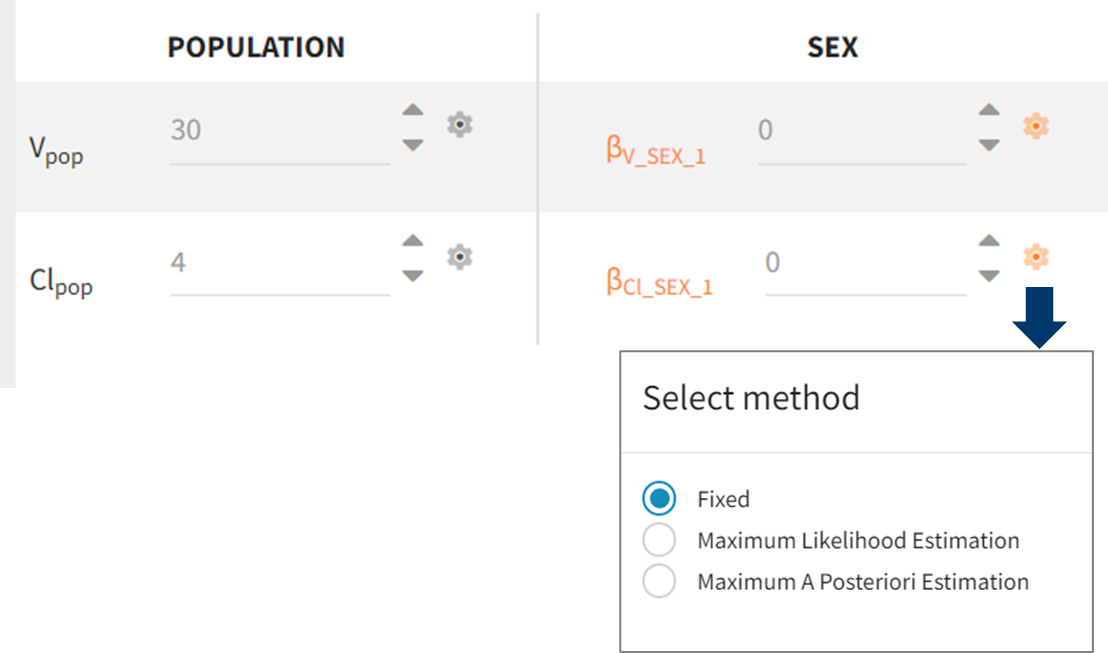 |
Running the Model and Related Tasks
The $ESTIMATION, $COVARIANCE, and $TABLE records are replaced by a graphical task manager in Monolix, which offers a more comprehensive and integrated set of tools.
Population Parameters: This is the main estimation task, equivalent to
$ESTIMATION. It uses the SAEM algorithm to find the maximum likelihood estimates of the population parameters.Individual Parameters (EBEs): This task calculates the Empirical Bayes Estimates (EBEs) of the parameters for each individual, along with the conditional standard deviations.
Standard Errors: This is the equivalent of
$COVARIANCE. It calculates the standard errors (and RSE%) for the population parameters by computing the Fisher Information Matrix.Likelihood: This task computes the log-likelihood of the model, equivalent to the final objective function value in NONMEM. It can be calculated via the more accurate (but slower) Importance Sampling or the faster Linearization method.
Plots: This task automatically generates a full suite of diagnostic plots (VPCs, individual fits, observation vs. prediction, residual plots, etc.), replacing the need for external tools like PsN and Xpose.
Integrated Tools: Monolix also includes built-in tools for tasks that require third-party software in the NONMEM world, such as Bootstrap for confidence intervals and Stepwise Covariate Modeling (SCM) for automated covariate searches.
Good luck, and welcome to the MonolixSuite!
Webinar
Here you can take a look at our webinar on this topic:
https://www.youtube.com/watch?v=PUCanvv5s0o&pp=ygURbm9ubWVtIHRvIG1vbm9saXg%3D
Here you can download the examples from the webinar:
