Categorical data models

Related resources on modeling categorical data in Monolix:

Columns used to define observations: formatting of categorical data in the MonolixSuite.
Categorical observation model : details on the different models for categorical data that can be used in Monolix and their syntax.

On the current page, we show examples of categorical data models from the Monolix demos.

Demos: categorical1_project, categorical2_project, markov0_project, markov1a_project, markov1b_project, markov1c_project, markov2_project, markov3a_project, markov3b_project

Ordered categorical data

categorical1_project (data = ‘categorical1_data.txt’, model = ‘categorical1_model.txt’)

In this example, observations are ordinal data that take their values in {0, 1, 2, 3}:

Cumulative odds ratio are used in this example to define the model

where

This model is implemented in categorical1_model.txt:

CODE

[LONGITUDINAL]
input = {th1, th2, th3}

DEFINITION:
level = { type = categorical,  categories = {0, 1, 2, 3},
  logit(P(level<=0)) = th1
  logit(P(level<=1)) = th1 + th2
  logit(P(level<=2)) = th1 + th2 + th3
}

A normal distribution is used for , while log-normal distributions for and ensure that these parameters are positive (even without variability). Residuals for noncontinuous data reduce to NPDEs. We can compare the empirical distribution of the NPDEs with the distribution of a standardized normal distribution:

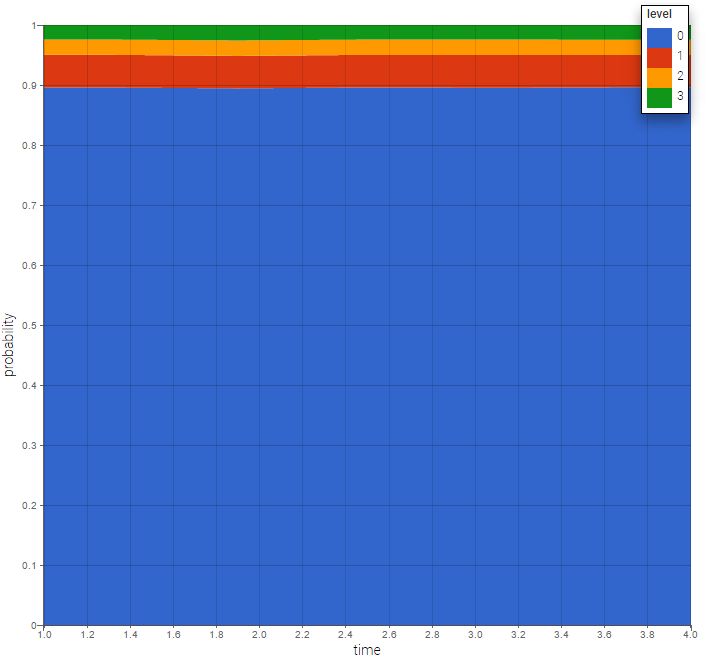
VPC’s for categorical data compare the observed and predicted frequencies of each category over time:

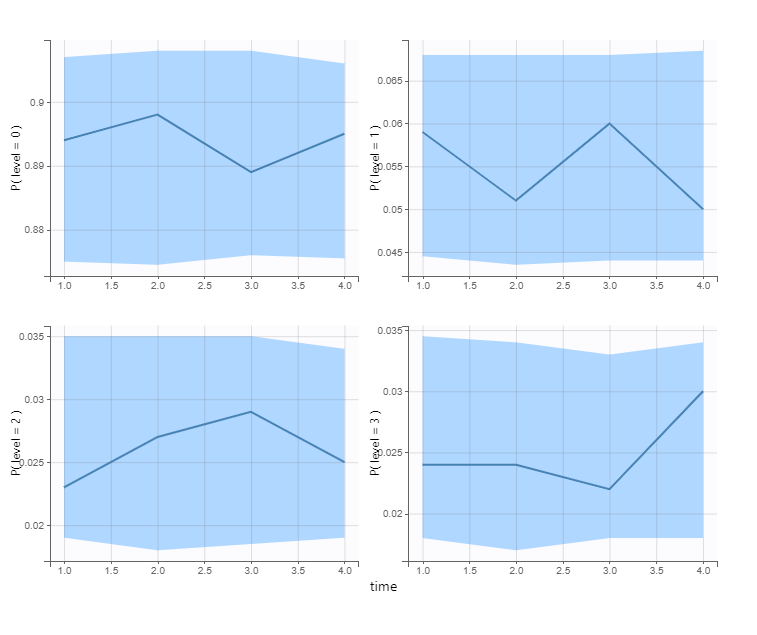
The prediction distribution can also be computed by Monte-Carlo:

Ordered categorical data with regression variables

categorical2_project (data = ‘categorical2_data.txt’, model = ‘categorical2_model.txt’)

A proportional odds model is used in this example, where PERIOD and DOSE are used as regression variables (i.e. time-varying covariates).

Discrete-time Markov chain

If observation times are regularly spaced (constant length of time between successive observations), we can consider the observations to be a discrete-time Markov chain.

markov0_project (data = ‘markov1a_data.txt’, model = ‘markov0_model.txt’)

In this project, states are assumed to be independent and identically distributed:

Observations in markov1a_data.txt take their values in {1, 2}.

markov1a_project (data = ‘markov1a_data.txt’, model = ‘markov1a_model.txt’)

Here,

CODE

[LONGITUDINAL]
input = {p11, p21}
DEFINITION:
State = {type = categorical,  categories = {1,2},  dependence = Markov
  P(State=1|State_p=1) = p11
  P(State=1|State_p=2) = p21
}

The distribution of the initial state is not defined in the model, which means that, by default,

markov1b_project (data = ‘markov1b_data.txt’, model = ‘markov1b_model.txt’)

The distribution of the initial state, , is estimated in this example

CODE

DEFINITION:
State = {type = categorical,  categories = {1,2},  dependence = Markov
  P(State_1=1)= p
  P(State=1|State_p=1) = p11
  P(State=1|State_p=2) = p21
}

markov3a_project (data = ‘markov3a_data.txt’, model = ‘markov3a_model.txt’)

Transition probabilities change with time in this example. We then define time varying transition probabilities in the model:

CODE

[LONGITUDINAL]
input = {a1, b1, a2, b2}
EQUATION:
lp11 = a1 + b1*t/100
lp21 = a2 + b2*t/100
DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
  logit(P(State=1|State_p=1)) = lp11
  logit(P(State=1|State_p=2)) = lp21
}

markov2_project (data = ‘markov2_data.txt’, model = ‘markov2_model.txt’)

Observations in markov2_data.txt take their values in {1, 2, 3}. Then, 6 transition probabilities need to be defined in the model.

CODE

[LONGITUDINAL]
input = {a11, a12, a21, a22, a31, a32}

DEFINITION:
State = {type = categorical, categories = {1,2,3}, dependence = Markov
  logit(P(State<=1|State_p=1)) = a11
  logit(P(State<=2|State_p=1)) = a11+a12
  logit(P(State<=1|State_p=2)) = a21
  logit(P(State<=2|State_p=2)) = a21+a22
  logit(P(State<=1|State_p=3)) = a31
  logit(P(State<=2|State_p=3)) = a31+a32
}

OUTPUT:
output=State

Continuous-time Markov chain

The previous situation can be extended to the case where time intervals between observations are irregular by modeling the sequence of states as a continuous-time Markov process. The difference is that rather than transitioning to a new (or the same) state at each time step, the system remains in the current state for some random amount of time before transitioning. This process is now characterized by transition rates from the state to the state .

markov1c_project (data = ‘markov1c_data.txt’, model = ‘markov1c_model.txt’)

Observation times are irregular in this example. Then, a continuous time Markov chain should be used in order to take into account the Markovian dependence of the data:

CODE

DEFINITION:
State = { type = categorical,  categories = {1,2}, dependence = Markov
  transitionRate(1,2) = q12
  transitionRate(2,1) = q21
}

markov3b_project (data = ‘markov3b_data.txt’, model = ‘markov3b_model.txt’)

Time varying transition rates are used in this example.

CODE

[LONGITUDINAL]
input = {c1, d1, c2, d2}

EQUATION:
q12 = max(0.001, c1 + d1*t/100)
q21 = max(0.001, c2 + d2*t/100)

DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
  transitionRate(1,2) = q12
  transitionRate(2,1) = q21
}

OUTPUT:
output=State

Initial state: by default, the probabilies for the initial state (first observation) are equal for all categories. For instance in case of 3 categories, .
To define different initial probabilities (e.g all individuals in State 1), they can be defined using the following syntax. Note that it is only necessary to define the probabilities of N-1 categories (as the last one can be derived from the sum being equal to 1).
CODE
```
[LONGITUDINAL]
input = {c1, d1, c2, d2}

EQUATION:
q12 = max(0.001, c1 + d1*t/100)
q21 = max(0.001, c2 + d2*t/100)

DEFINITION:
State = {type = categorical, categories = {1,2}, dependence = Markov
  P(State_1=1)= 1
  transitionRate(1,2) = q12
  transitionRate(2,1) = q21
}

OUTPUT:
output=State
```