Calculating the half-life

The half-life is usually not part of the estimated parameters but it often needs to be reported. It presents the advantage of having units of time and being easy to understand. The terminal plasma half-life is the time required to divide the plasma concentration by two after reading pseudo-equilibrium. It is especially relevant to multiple dosing regimens, because it controls the degree of drug accumulation and the time taken to reach equilibrium. For a more detailed overview, please refer to:

Toutain P.L, Bousquet-Melou A. Plasma terminal half-life, J. vet. Pharmacol. Therap. 27, 427-439, 2004

This documentation page explains the half-life formulas and how to modify the Monolix or Simulx models to calculate it.

Half-life formulas

One-compartmental model

For a drug captured by a model with one compartment and linear elimination, and without flip-flop kinetics, the half-life is calculated as:

with the elimination rate, the clearance and the volume of distribution. Note that so you might also find the formula written with this value.

Two-compartmental model

For a drug captured by a model with one compartment and linear elimination, the half-life correspond to the slope of the second part of the curve on a log-concentration over time plot, once pseudo-equilibrium is achieved. The slope of the terminal (second) phase is usually called , the first slope and the intercepts A and B.

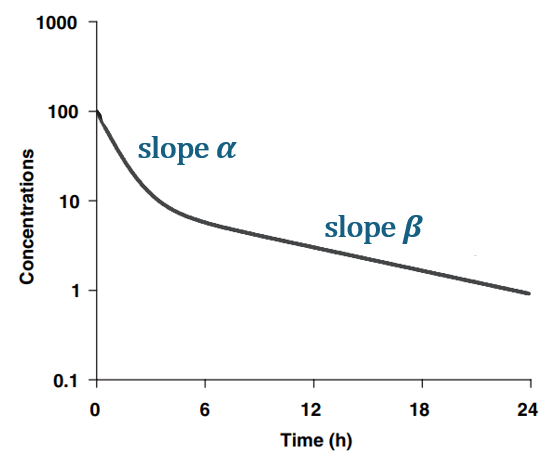
The parametrization of the 2-compartment model with (A, B,) is an alternative parametrization compared to the parametrization with (k, V, k12, k21) or (Cl, V, Q, V2).

It is possible to convert between these different parametrizations using the following formulas:

The half-life corresponds to the terminal phase and is defined as: