Cost, AIC and BIC

Cost function

The cost function that is minimized in the optimization performed during CA is described here. The cost is reported in the result tables after running CA, as individual cost in the table of individual parameters, and as total cost in a separate table, together with the likelihood and additional criteria.

Formulas for the cost function used in PKanalix are derived in the framework of generalized least squares described in the publication Banks, H. T., & Joyner, M. L. (2017). AIC under the framework of least squares estimation. Applied Mathematics Letters, 74, 33-45, with an additional scaling to put the same weight on different observation types.

The total cost function, shown in the cost table in the results, is a sum of individual costs per occasion (that is, summed over id-occ):

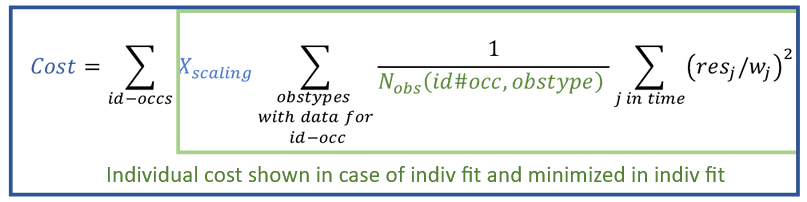
where in the above formula:

• denotes the number of observations for one individual, one occasion and one observation type (i.e., one model output mapped to data, such as parent and metabolite, or PK and PD, see here).

• are residuals at measurement times , where are the predictions for each time point , and are the observations from the dataset at that time.

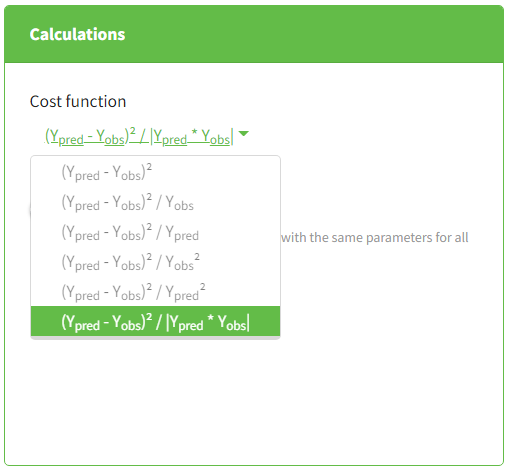
• are weights, selected from the following: , , , , , depending on denominator of the selection in CA task > Settings > Calculations, as explained in this tutorial video.

is a scaling parameter given by:

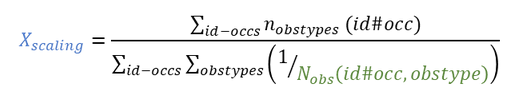
whereis the number of observation IDs mapped to a model output for one individual and one occasion. Note that if there is only one observation type (corresponding to one observation ID),and the cost function is a simple sum of squares over all observations, weighted by the weights.

Likelihood

The likelihood is not directly used in the optimization for CA, but it is possible to derive it based on the optimal cost obtained with the following formula (details in Banks et al.):

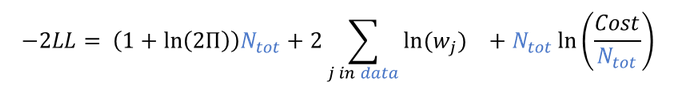
where

• stands for ,

• is the total number of observations for all individuals, all occasions and all mapped model outputs,

• are the weights as defined above.

Additional Criteria

Additional information criteria are the Akaike Information Criteria (AIC) and the Bayesian Information Criteria (BIC). They can be used to compare models. They penalize -2LL by the number of parameters estimated, including the number of model parameters used for the optimization,, the total number of observations, , and the number of observations for every subject-occasion,. This penalization enables comparing models with different levels of complexity. Indeed, with more parameters, a model can easily fit better (lower -2LL), but with too many parameters, a model loses predictive power and confidence in the parameter estimates. If not only the -2LL, but also the AIC and BIC criteria decrease after changing a model, it means that the increased likelihood is worth increasing the model complexity.

This formula simplifies if the “pooled fit” option is selected in the calculation settings of the CA task:

AIC derivation in the case of individual fits

The total AIC for all individuals penalizes -2LL with 2 x the number of parameters used in the optimization. For the structural model, we estimateparameters, whereis the number of parameters in the structural model andis the number of subject-occasions (since there is a set of parameters estimated for each id#occ). For the statistical model, we also implicitly estimate a parameter , which is the variance of the residual error model shared by all individuals (it is derived using the sum of squares of residuals as described in Banks et al.). Therefore, AIC penalizes -2LL by .

BIC derivation in the case of individual fits

The total BIC penalizes -2LL by (number of parameters) x ln(number of data points). In this case, we should distinguish between the data for each id#occ, which is used to estimateparameters, and the data for all individuals, which is used together to estimate the residual variance . To penalize each individual’s data in the estimation of, we add the term for each id#occ. To penalize the estimation of the error model parameter with all the observations (substitution of as described in Banks et al.), we add the term .