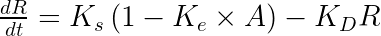K-PD models

Usual PK-PD models describe the relationships between dose regimens, drug concentration and effect (or response). They are applied when both the drug concentration and the effect can be measured. However situations exist where the concentration PK data is not available. This may for instance be the case for phase III clinical trials or pediatric studies. In this case K-PD models can be used: the drug concentration-effect relationship model is kept, but the (unobserved) PK profile is assumed to have a simple shape. In comparison to dose-response studies which directly link the (constant) dose to the PD response, K-PD models permit to capture PD profile that varies over time as a consequence of the underlying time-varying PK profile.

Although not being the first published example of K-PD model, the usual reference is:

Jacqmin, P., Snoeck, E., Schaick, E. A. Van, Gieschke, R., Pillai, P., Steimer, J., & Girard, P. (2007). Modelling Response Time Profiles in the Absence of Drug Concentrations : Definition and Performance Evaluation of the K-PD Model. Journal of Pharmacokinetics and Pharmacodynamics, 34(1). 

Mlxtran code for K-PD models

The effect of the drug on the response can be as diverse as presented in the indirect response models and direct response models examples. We here focus on the case of an indirect response where the drug decreases the response production rate. 

Formulation by Jacqmin et al.

The authors in Jacqmin et al. describe the model in the following way: “A virtual compartment representing the biophase in which the concentration is in equilibrium with the observed effect is used to extract the (pharmaco)kinetic component from the pharmacodynamic data alone. Parameters of this model are the elimination rate constant from the virtual compartment (KDE), which describes the equilibrium between the rate of dose administration and the observed effect, and the second parameter, named EDK50 which is the apparent in vivo potency of the drug at steady state.

The equations read:

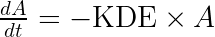
with A the drug amount, R the response, KDE the drug elimination rate, Ks the response synthesis rate, Kd the response disappearance rate constant.  EDK50 represents the potency of the drug and also corresponds to EDK50 constant corresponds to the product of the EC50 and the clearance.

The corresponding Mlxtran code is:

[LONGITUDINAL]
input={Ks,Kd,KDE,EDK50}

PK:
depot(target=A)

EQUATION:
; initialization
t_0 = 0
A_0 = 0
R_0 = Ks/Kd

; ODEs
ddt_A = - KDE*A
ddt_R = Ks * (1 - (KDE*A)/(EDK50 + (KDE*A))) - Kd*R

OUTPUT:
output = {R}

Note that the only output is the response R, as only the response has been measured and recorded in the data set.

Alternative formulation

For some applications, the interpretation of the parameters of the Jacqmin model may be difficult. It is also unusual the consider that it is the rate at which the drug disappear (IR) that drives the effect on the response. We thus propose an alternative formulation of the same model.

We start by writing the model using the usual (and physiologically relevant) effect of the drug concentration on the response:

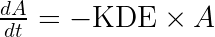
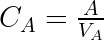
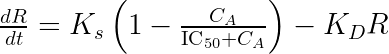
This set of equations can be rewritten into:

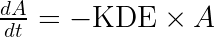
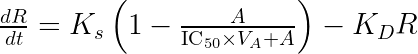
using the fact that . When the drug concentration is observed, it is possible to identify both and  separately because  influences the observed drug concentration. However when the drug concentration is not measured, it is not possible to identify both  and , but only the product of the two. The unidentifiability of the volume of distribution is explore visually and interactively in the next section.

We thus introduce and write our final model as:

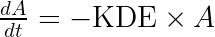
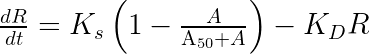
The parameter  can simply be interpreted as the product of the usual and the volume of distribution of the drug.

The mlxtran model reads:

[LONGITUDINAL]
input={Ks,Kd,KDE,A50}

PK:
depot(target=A)

EQUATION:
; initialization
t_0 = 0
A_0 = 0
R_0 = Ks/Kd

; ODEs
ddt_A = - KDE*A
ddt_R = Ks * (1 - A/(A50 + A) ) - Kd*R

OUTPUT:
output = {R}

The model can also be written using macros for the (P)K part. When macros are used, the PK part of the model will be calculated using the analytical solution while the PD part will be solved using the ODE solver.

[LONGITUDINAL] 
input={Ks,Kd,KDE,A50} 

PK: 
compartment(cmt=1, amount=A)
iv(cmt=1)
elimination(cmt=1, k=KDE) 

EQUATION: 
; initialization 
t_0 = 0 
R_0 = Ks/Kd 

; ODEs 
ddt_R = Ks * (1 - A/(A50 + A) ) - Kd*R 

OUTPUT: 
output = {R}

Extensions

If data is sufficient to allow for the estimation of the additional parameters, the model can be extended, for instance in the following directions:

• more complex profile for the drug concentration, for example with a first-order input rate. In this case, the additional input arguments can be directly given in the depot macro;

• sigmoidal Emax or Imax model with a hill exponent;

• Emax or Imax value different from one.

The model can also be adapted to consider K-PK models, where two drugs interact and only one of the two is measured.

Simplifications

The use of an Emax or Imax model is only suited if the dose range is sufficiently large to cover both the linear and saturating part of the Michaelis-Menten curve. If concentrations are always smaller than the EC50, the model simplifies to: