Absorption delays via sigmoid absorption, transit compartments or Weibull absorption
Absorption delays are common after oral administrations. They reflect the time needed for drug dissolution and/or for transit to the absorption site (Savic et al., 2007). A simple option is to model this delay via a lag time (i.e the absorption starts after a delay). However, this may not properly capture the concentration-time profile and the progressive appearance of the drug to the absorption site. Several approaches have been used to model a progressive delay:
sigmoid absorptions, which assume a zero-order input into the depot compartment followed by a first-order absorption from the depot to the central compartment.
transit compartment models, which describes the absorption as a multiple step process with a chain of pre-systemic compartments
Weibull absorptions, which describe the change in the absorption rate ka in a phenomenological way via a Weibull function. test..
Sigmoid absorption
The sigmoid model is also called “sequential zero order + first order absorption” where sequential is mant in terms of order of compartments. The absorption from the depot to the central compartment occurs via a usual first-order process with parameter ka. To introduce the delay, the dose is put into the depot compartment progressively, via a zero-order process of duration Tk0 (instead of a bolus). The model scheme is the following:
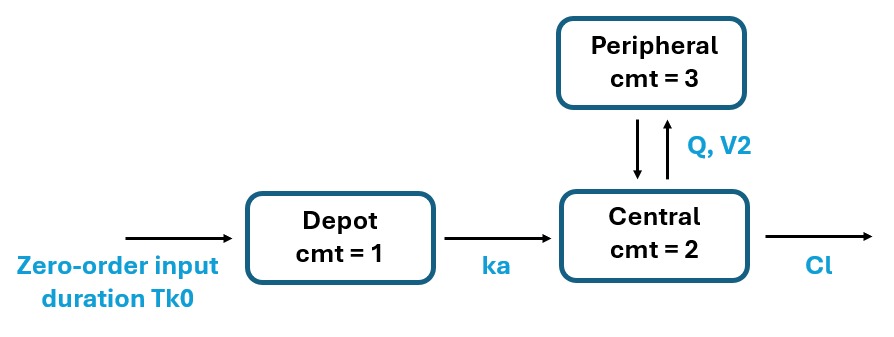
The sigmoid absorption model presents the advantage of introducing a single additional delay parameter and having an analytical solution. For the analytical solution to be used, it is necessary to add a dummy elimination with clearance equal zero from the depot macro.
Note that in comparison to Nonmem, it is not necessary to add a RATE=-1 or RATE=-2 column in the dataset.
The mlxtran code reads:
[LONGITUDINAL]
input = {Tk0, ka, V, Cl, Q, Vp}
PK:
; depot compartment
compartment(cmt = 1, amount = Ad)
; zero order input in depot (cmt=1)
absorption(cmt = 1, Tk0)
; elimination from depot is required for analytical solution but can be set to zero
elimination(cmt = 1, Cl=0)
; central compartment
compartment(cmt = 2, volume = V, concentration = Cc)
; first order absorption from depot to central
transfer(from = 1, to = 2, kt = ka)
; elimination from central compartment
elimination(cmt = 2, Cl)
; optional peripheral compartments (one or two peripheral compartments)
peripheral(k23=Q/V, k32=Q/Vp)
OUTPUT:
output = {Cc}If a bioavailability F needs to be considered, it can be added in the absorption() macro as:
absorption(cmt = 1, Tk0, p=F)Transit compartments
Transit compartment can easily be implemented using the oral macro (when describing the model using macros) or the depot macro (when describing the model using ODEs), by adding the parameters Mtt and Ktr in addition to the usual absorption rate ka. Mtt represents the mean transit time and Ktr the transit rate between compartments. These two parameters are related via the number of compartments n:
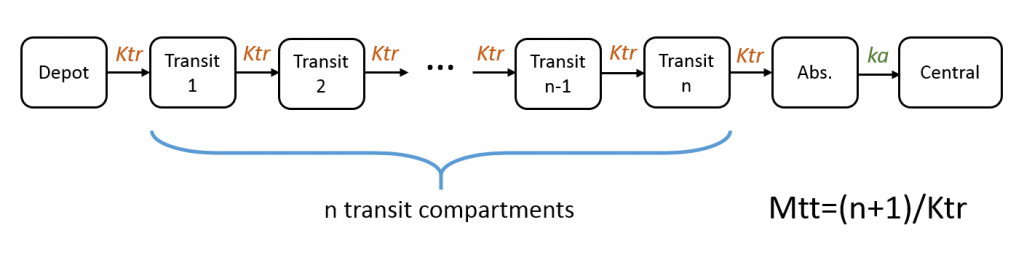
In case of multiple doses, the amounts in the depot, transit and absorption compartments are reset at each new doses. Thus the implementation is valid only if the dose is fully absorbed before the next dose administration. The amount in the central (and possibly other compartments) is not reset and can accumulate.
Example with model based on macros
[LONGITUDINAL]
input={ka, Mtt, Ktr, V, k}
PK:
compartment(cmt=1, volume=V, concentration=Cc)
oral(cmt=1, Mtt, Ktr, ka)
elimination(cmt=1,k)
OUTPUT:
output = CcExample with model based on ODEs
The entire absorption process is handled by the depot macro, which reads the dose information in the data set and applies an input rate to the target Ac corresponding to an oral administration with transit compartments.
[LONGITUDINAL]
input={ka, Mtt, Ktr, V, k}
PK:
depot(target=Ac, ka, Mtt, Ktr)
EQUATION:
t_0 = 0
Ac_0 = 0
ddt_Ac = - k * Ac
Cc = Ac/V
OUTPUT:
output = CcWeibull absorptions
Despite the lack of physiological basis, the Weibull model is appreciated for its flexibility (Zhou et al, 2003). In practice, it is rarely used. We here demonstrate the implementation of one Weibull function models. The extension to two Weibull functions is straightforward. The time-varying absorption rate is:
|
|
The model requires to be written as an ODE system with a depot compartment and at last a central compartment. The transfer of matter from the depot compartment to the central compartment is described using a time-varying rate constant. To allow for multiple doses, the time is calculated with respect to the time of the last dose, using the tDose keyword. Note that only one type of administration (only oral or only iv for instance) is allowed per individual, as the tDose keyword doesn’t distinguish between different administration types ADM.
The alpha parameter describes the delay, while the beta parameter influences the steepness of the absorption phase.
[LONGITUDINAL]
input={beta, alpha, V, k}
PK:
depot(target=Ad)
EQUATION:
t_0 = 0
Ad_0 = 0
Ac_0 = 0
ddt_Ad = -Ad * (beta/alpha)*(max(0,t-tDose)/alpha)^(beta-1)
ddt_Ac = Ad * (beta/alpha)*(max(0,t-tDose)/alpha)^(beta-1) - k*Ac
Cc = Ac/V
OUTPUT:
output = Cc