In this example, we approximate the response of PCA to warfarin with a neural network.
This example is based on the following publication:
Bräm, D. S., Steiert, B., Pfister, M., Steffens, B., & Koch, G. (2024). Low‐dimensional neural ordinary differential equations accounting for inter‐individual variability implemented in Monolix and NONMEM. CPT: PSP
Introduction
A neural network (NN) is a highly flexible function with a lot of parameters. These parameters can be optimized using training data. We can use neural networks to approximate any other function, according to the universal approximation theorem.
As neural networks are usually quite complex and contain a large number of parameters, the NN calculations are usually automated using specialized software packages. However, if a NN is sufficiently small, we can write it as an explicit function of the form:
The NN above consists of one layer of K neurons. The output
is calculated as the sum of linear functions of the input
.
is thus a stepwise linear function. The
parameters are representing the weights and the
parameters the intercepts (also called bias).
In addition, neural networks can be used within ODE-based models. Neural ODEs (NODEs) can be defined as differential equations with a neural network on the right-hand side of the equation, instead of a mechanism based function.
If the neural network is small, we can write the neural ODE by substituting (1) into (2) and estimate the parameters
and
using Monolix.
Example
The data set, model file and project files from this case study can be downloaded here: NODE_example.zip
Let’s take a look at the example of warfarin PKPD data set that includes warfarin concentrations and platelet coagulant activity (PCA) as response. Wihtout using neural ODEs, the PK part of the data can be modeled with a one-compartment model with delayed first order absorption and linear elimination, while the PD part of the data can be modeled with an indirect response model with inhibition of the production term:
Let’s assume that the PK model is already known, but the PD model is unknown. We can approximate the response of PCA as a turnover model with a neural network to characterize the shape of the inhibition of the production by the PK concentration:
Structural model
The Mlxtran code for such a model combines the pkmodel() macro for the PK, a variable fNN for the neural network and a turnover model using the neural network fNN for the response R:
[LONGITUDINAL]
input = {Tlag, ka, V, Cl, R0, W11,W12,W13,W14,W15,b11,b12,b13,b14,b15,W21,W22,W23,W24,W25,b21,kout}
PK:
;====== PK part of the model
; PK model definition
Cc = pkmodel(Tlag, ka, V, Cl)
EQUATION:
;====== PD part of the model
kin = kout * R0
; Initial values
R_0 = R0
; Parameter transformation
h1 = max(0, W11 * Cc + b11)
h2 = max(0, W12 * Cc + b12)
h3 = max(0, W13 * Cc + b13)
h4 = max(0, W14 * Cc + b14)
h5 = max(0, W15 * Cc + b15)
fNN = min(W21 * h1 + W22 * h2 + W23 * h3 + W24 * h4 + W25 * h5 + b21, 1)
; ODE for the response
ddt_R = kin * (1 - fNN) - kout * R
OUTPUT:
output = {Cc, R}
Note that the min() and max() functions ensure that fNN stays between 0 and 1, such that the inhibition term (1-fNN) remains positive.
Statistical model
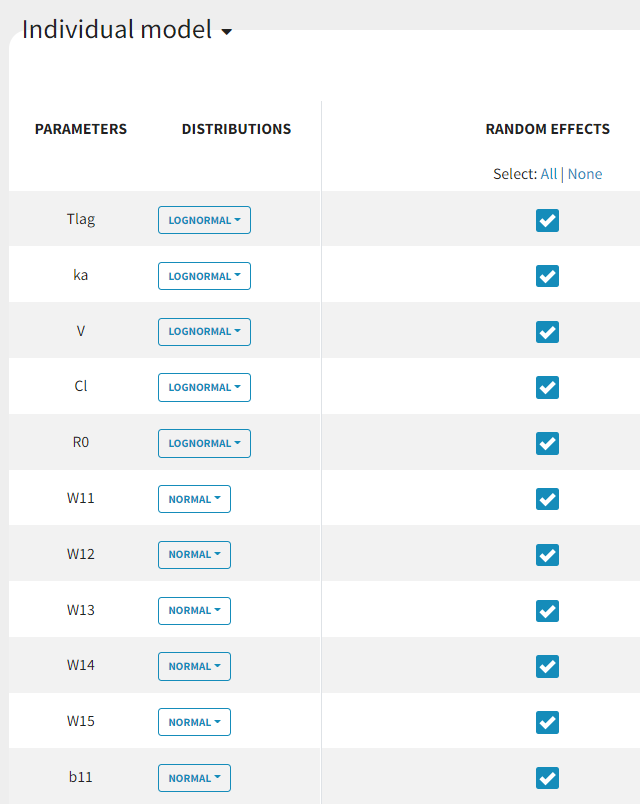
Since
and
parameters can be both positive and negative, we need to change the distribution of those parameters to normal. Random effects are initially included on all parameters and this will be adjusted afterwards.
Population parameter task settings
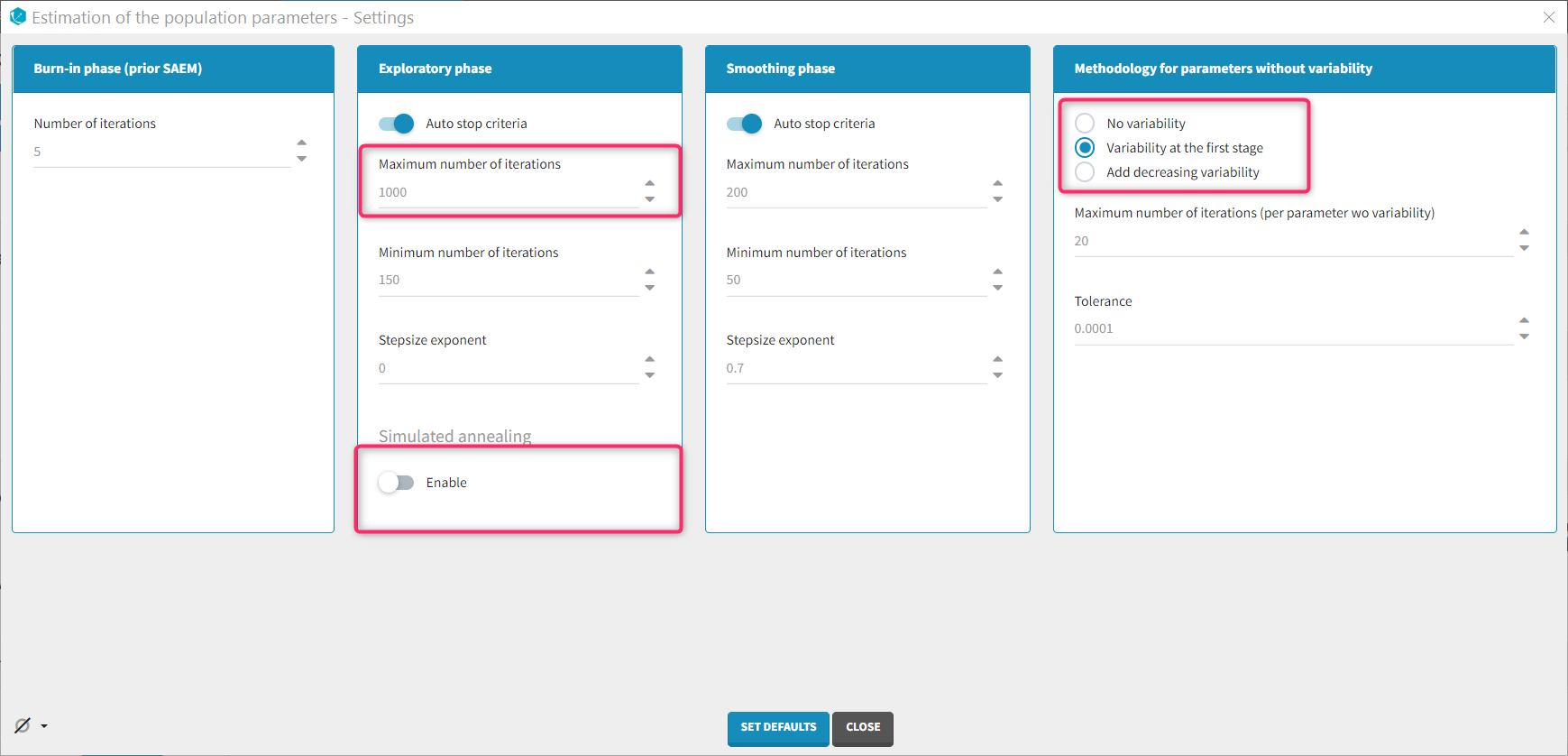
As there are many parameters to estimate, the estimation may require more iterations than usual. The maximum number of iterations can be increased, for instance to 1000 iterations.
Including random effects on all parameters probably leads to over-parametrization. In order to identify parameters on which the random effects can be removed, it is possible to disable the “simulated annealing” option. This will allow the unnecessary omega parameters to converge to zero. In the next run, the random effects of these parameters can be removed.
Parameters without random effects are not estimated using SAEM and several estimation methods are available for parameters without variability. It is worth trying both the “no variability” and the “variability at the first stage” methods.
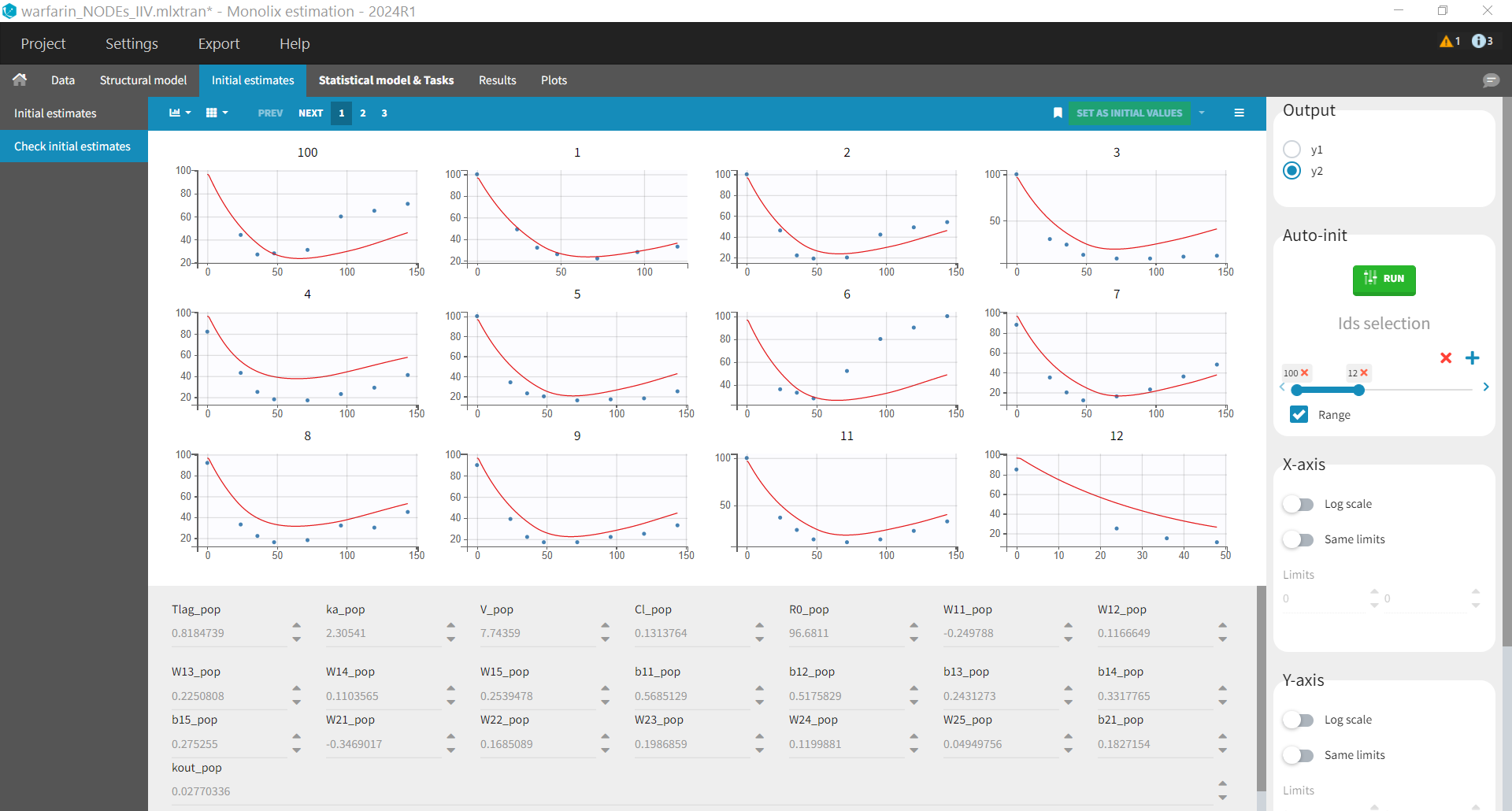
Initial values
When initializing parameters, it is important to notice that for each node (i.e neuron) of the neural network, the term max(0, W * Cc + b) will be equal to 0 if
. This is a bad initial value as small changes in
and
are likely to produce the same value 0, which makes it difficult for the optimization algorithm to know if which direction to go. So parameters should be initialize so that the sets of parameters
and
are such that
. We can initialize the values by using the auto-init feature of Monolix, combined with a manual adjustment to ensure that parameters satisfy the mentioned criteria.
For the standard deviation of the random effects (omega parameters), they are set to 1 in Monolix by default, which corresponds to 100% variability in case of a log-normal distribution. In our case, we are working with normal distributions and our initial values for
and
are in the range 0.1-0.5. Thus the initial omega values can be set to 0.1-0.5, which corresponds to 100% variability of the normal distribution.
Results
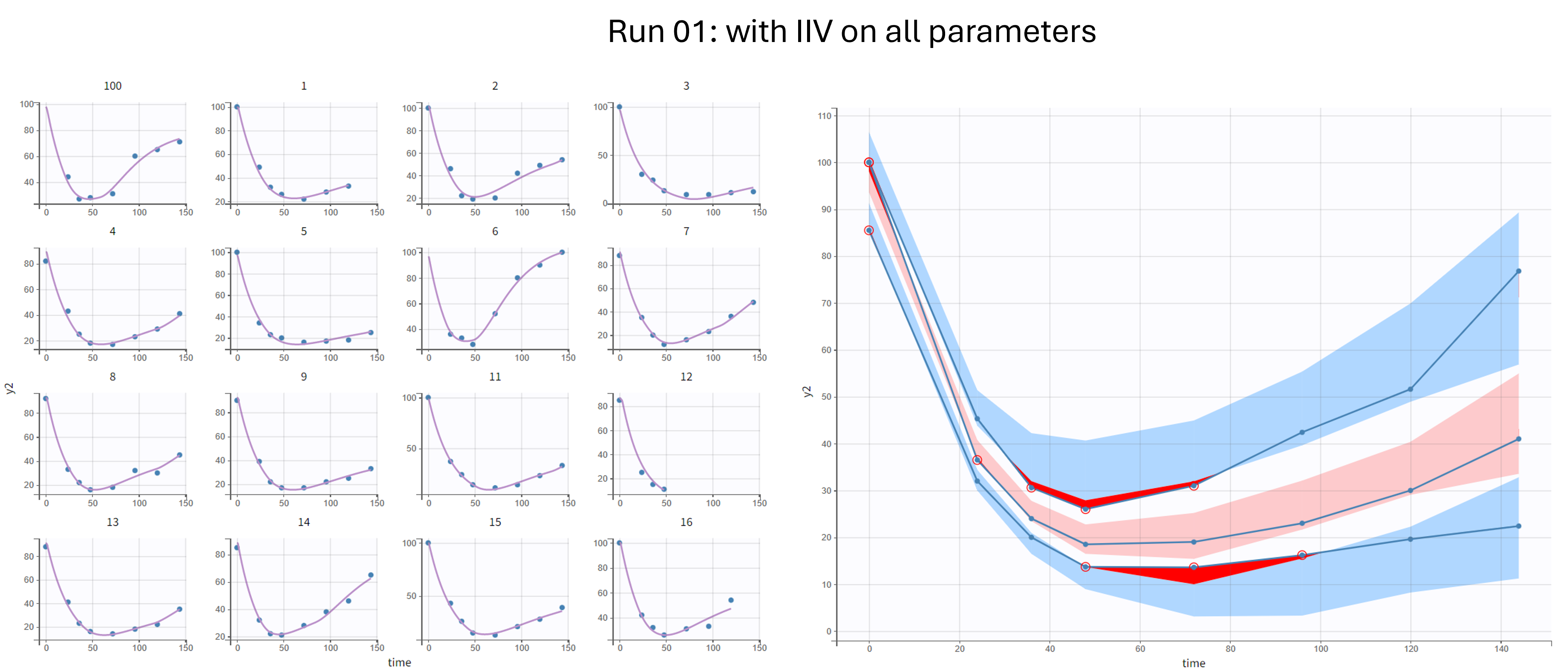
Run 01 - with IIV on all parameters
In the first run, we keep the random effects on all parameters. This model leads to good individual fits and a reasonable VPC, but is likely overparametrized.
Run 02 - with IIV on all parameters and no simmulated annealing
In the second run, we use the estimated from the previous run as initial values. In order to identify parameters on which the random effects can be removed, we disable the simulated annealing in the “Population parameters” task settings. This allow the omega parameters to converge to zero if random effects are not needed.
In the results of estimated population parameters, we see that most NN parameters have a coefficient of variation below 2% except W11 and b21. We thus decide to remove the random effects on all parameters except those two.
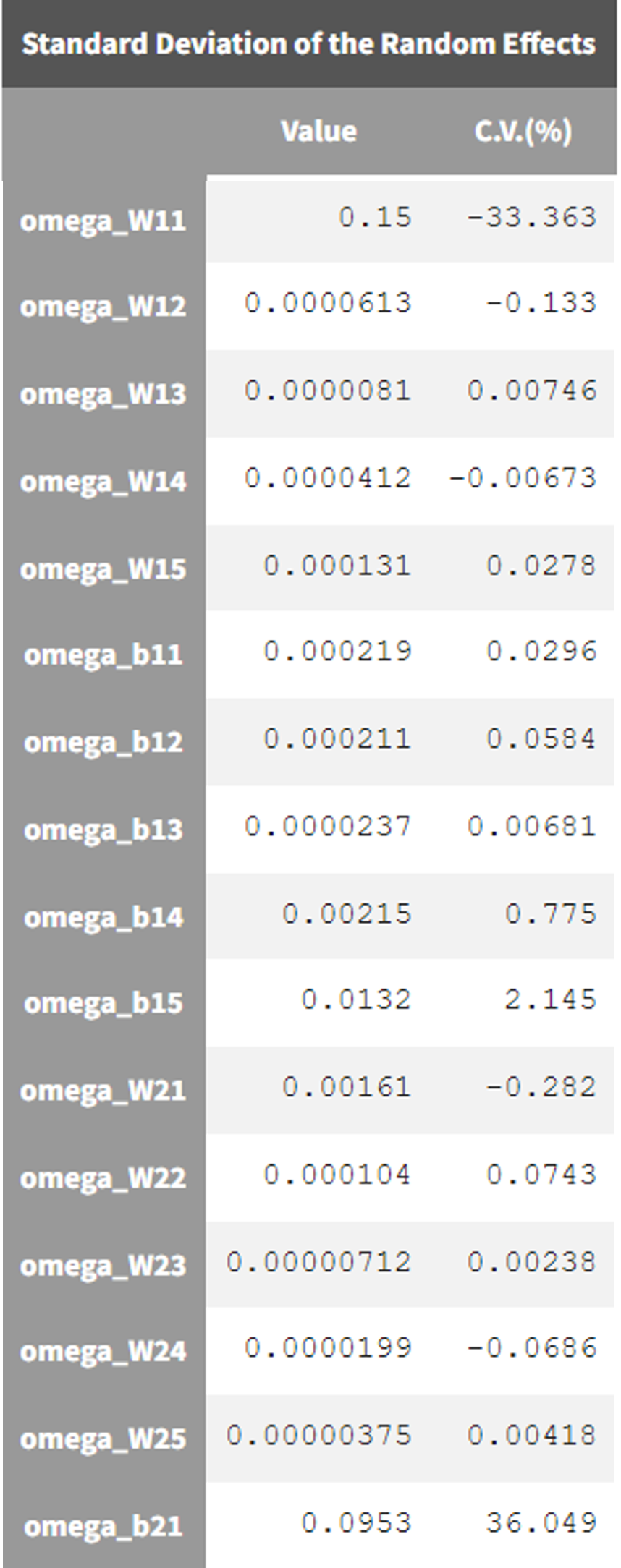
Run 03 - with IIV on W11 and b21 - method “no variability”
Parameters without random effects require a separate estimation method. We first try the default option called “no variability”. In this case, the parameters without IIV are estimated using the deterministic Nelder-Mead algorithm.
The individuals fits and VPC looks similar to run 01.
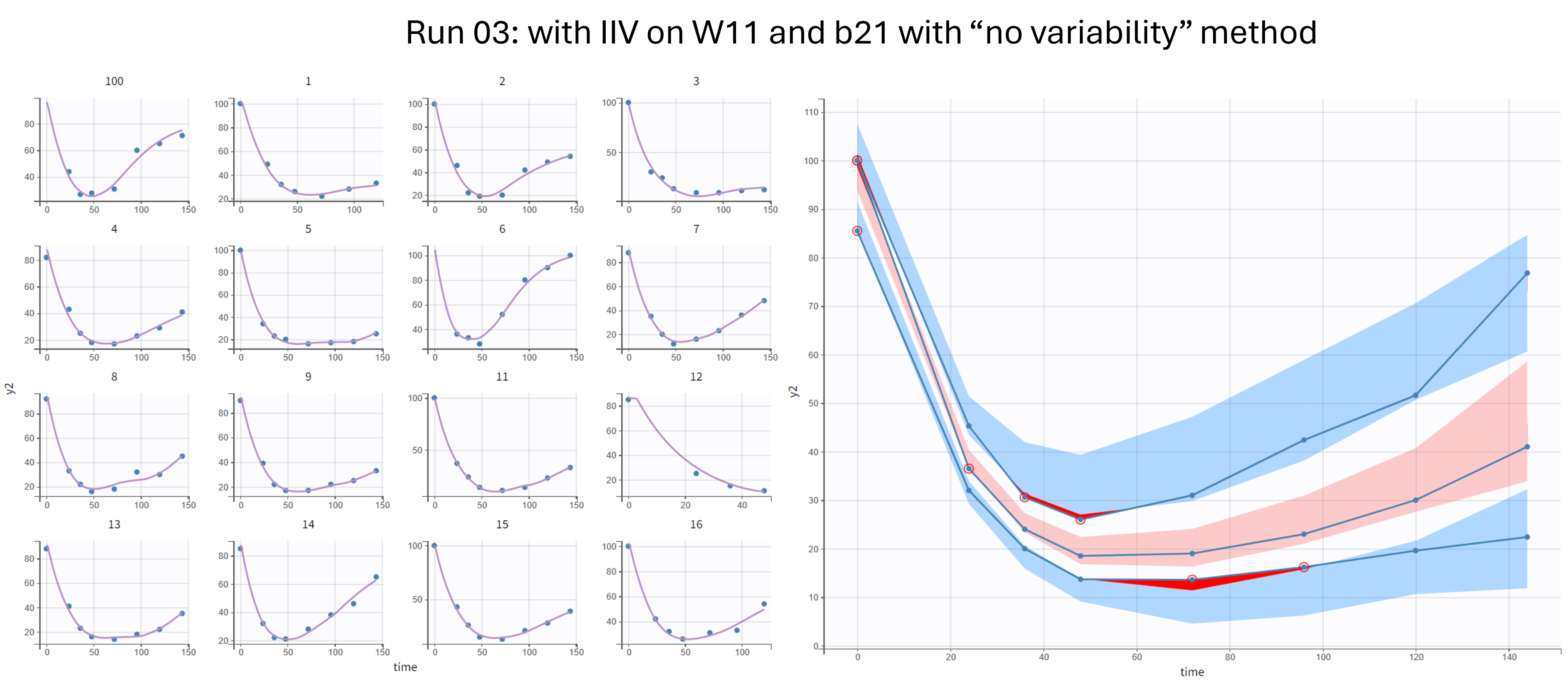
Run 04 - with IIV on W11 and b21 - method “Variability at the first stage”
We also first try the option called “variability at the first stage”. In this case, in the exploratory phase, random effects are added on all parameters in the background such that the parameters without IIV are estimated using SAEM as usual. The omega parameters are progressively forced to zero, in order to obtain a model wihtout random effects at the end of the exploratory phase. In the smoothing phase, the deterministic Nelder-Mead algorithm is used to adjust the values.
With this method, the results are similar. The individuals fits and VPC looks similar to run 01 and 03.
Conclusion
Neural ODEs can be used in Monolix as a data-driven modeling approach, which can be useful to model data when the mechanism based models partially or completely fail to describe the data.
However, users should be careful when diagnosing and interpreting neural ODE models, as the diagnostic and model refinement procedures differ from the classical approach. With the classical population approach, modelers stride to find a set of parameters in the global minimum of the objective function. When working with neural networks, given the high number of parameters and high flexibility, the goal is to find a set of parameters in a good local minimum of the objective function.
This means that some of the usually applied diagnostic methods are not applicable when using the neural ODE approach. Mainly, high RSEs and correlations in the FIM are expected and do not require model refinement. In case of bad fit, model refinement can be done by altering initial values and changing methods for the estimation of the parameters with no inter-individual variability (“No variability” or “Variability at the first stage”).

